Welcome to the Onshape forum! Ask questions and join in the discussions about everything Onshape.
First time visiting? Here are some places to start:- Looking for a certain topic? Check out the categories filter or use Search (upper right).
- Need support? Ask a question to our Community Support category.
- Please submit support tickets for bugs but you can request improvements in the Product Feedback category.
- Be respectful, on topic and if you see a problem, Flag it.
If you would like to contact our Community Manager personally, feel free to send a private message or an email.
Best Of
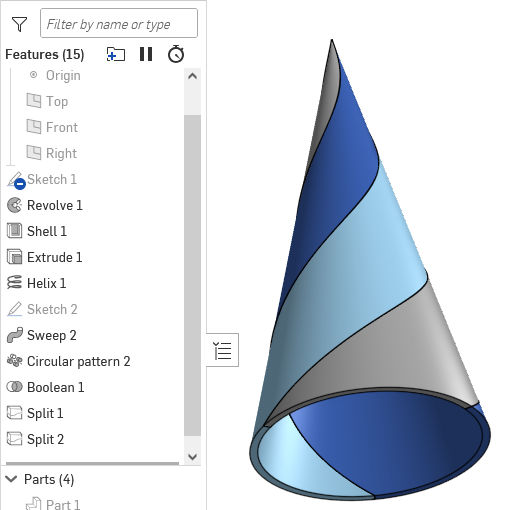
Re: Splitting a hollow cone by a helix
The split dialog box suggests that the Split tool only allows for splitting an entity into two pieces in that it asks for a singular entity to split with and asks whether or not to keep both pieces. Perhaps thickening the surfaces to .001" and using the Boolean (subtract) tool to create the three parts would satisfy your desired results. - Scotty
Re: Extrude along a angled surface
Select the edge face as the sketch plane. - Scotty
Re: How to make cutouts on sphere follow the curve?
Hey Cindy. Here is something very clever. - Scotty
Re: Fully-defined sketches: what are they, and why care?
Before, you'd look for the blue geometry.
 _anton
_anton
Re: Invalid Normal Until a More-Distant Point is Used
I'll kinda sidestep your question a bit to get at your goals. The cross product of parallel vectors should be a zero vector with no direction, so the case where it works seems like the odd one out. Might be a floating point precision thing making the second case just off enough to get a result from cross()? In any case, if you just need any perpendicular vector try perpendicularVector() instead of cross(). If you need to know for sure which direction that normal will go, then you could align it to something else known.
Re: Export rules does not apply to multiple exported files inside ZIP file
Re: Export rules does not apply to multiple exported files inside ZIP file
Re: Splitting a hollow cone by a helix
I suppose joining the 3rd surface creates a sorta zero thickness sorta situation, so it can't do it. would have to be done in 2 splits then.
 MDesign
MDesign
Re: Splitting a hollow cone by a helix
I don't think it's a zero thickness situation, more like a front side vs back side situation. If you have two surfaces sharing an edge they both can agree on matching the orientation of the faces on both sides of said edge. (Unless you do a mobius strip or something like that) As soon as you add a third surface meeting said edge you've guaranteed that face #3 is going to have opposing normals to one of the other two faces sharing the set. Imagine doing a split then flipping the handles to try to decide which "side" of the split to keep. How do you define a "side" when you have a group of face normals that opposes itself?
Re: Splitting a hollow cone by a helix
@Derek_Van_Allen_BD that's much better explanation… I knew it was something like that that I was trying to get at but couldn't put the words to it. Thank you.
 MDesign
MDesign