Welcome to the Onshape forum! Ask questions and join in the discussions about everything Onshape.
First time visiting? Here are some places to start:- Looking for a certain topic? Check out the categories filter or use Search (upper right).
- Need support? Ask a question to our Community Support category.
- Please submit support tickets for bugs but you can request improvements in the Product Feedback category.
- Be respectful, on topic and if you see a problem, Flag it.
If you would like to contact our Community Manager personally, feel free to send a private message or an email.
Fitting surface to complex iterative approximation? [co-planar, tapered helical spur gears]
 Tim_Blakely
Member Posts: 3 PRO
Tim_Blakely
Member Posts: 3 PRO
I've been toying around with something similar to @rodrigo_rivas_costa 's Bevel Gears script, but for spur + helix + tapered + inner [ring] gears. Think helical spur gears like you'd get from the usual script, but with a taper towards the outer edge. 

Analytical solutions like Rodrigo's are beyond my math skills, but I've been messing around with some iterative approaches that come close. The trick with the additional taper is that the module on the outer surface is noticeably smaller than at the center of the gear, which means - particularly for inner/ring gears - that co-planar meshing gears (not the 90-degree bevel gears in Rodrigo's script) have a pretty complex surface to mesh with along the surface of the tooth.

I can approximate the meshing pattern by opPattern sweeping along both radii:

Which gives a good approximation of the mating surface. For example, with no taper you get a typical involute pattern on the outer surface since the modules along the center/outside match:

With an additional taper (pitch diameter outer vs inner illustrated here) the meshing curve is no longer involute:
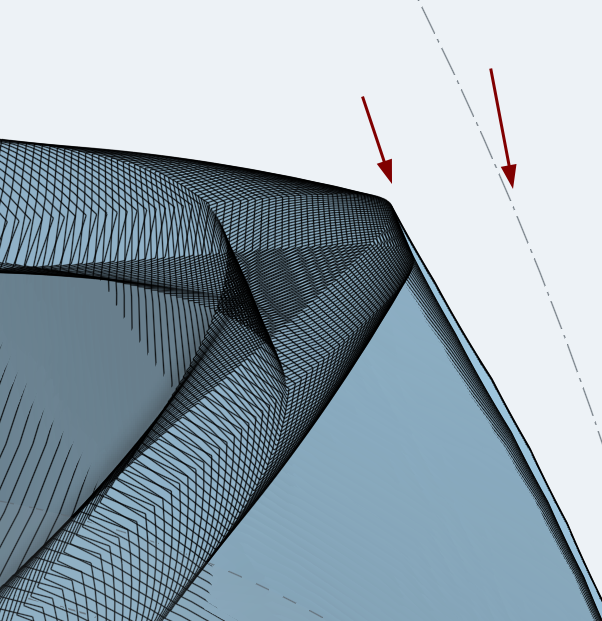
I can kind of get this to work by doing successive opBoolean calls to create an approximation of the total curve, but the aliasing can get pretty bad without a very small step size:
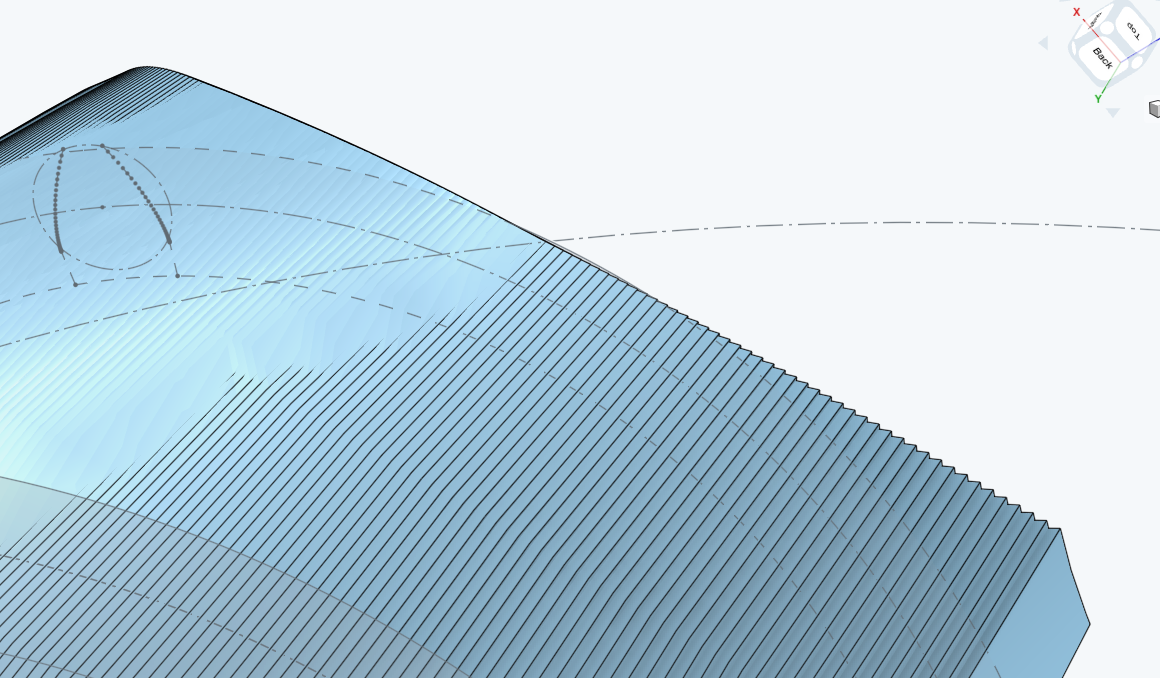
The whole goal is to create a body that will act as the gear cutter for a ring gear, ensuring that there's no interference. Beyond the fact that opBoolean times out if you try to union more than a few surfaces, the whole recalculation is quite compute intensive and takes quite a long time to recompute (O(minutes)). Is there a way to fit a surface to this kind of approximation to avoid both the boolean ops and the aliasing? Or, alternatively, is there another approach that I'm missing that would simplify this iterative approach? I'll readily admit I'm quite new at FeatureSript; I only started messing with it for the first time this morning, so it's entirely possible there's an easier way to accomplish what I'm trying to do.
Side note: Might want to update the documentation on opLoft to include the fact that you can add a spine, but only if you also enable addSections... took me a while to figure that out


Analytical solutions like Rodrigo's are beyond my math skills, but I've been messing around with some iterative approaches that come close. The trick with the additional taper is that the module on the outer surface is noticeably smaller than at the center of the gear, which means - particularly for inner/ring gears - that co-planar meshing gears (not the 90-degree bevel gears in Rodrigo's script) have a pretty complex surface to mesh with along the surface of the tooth.

I can approximate the meshing pattern by opPattern sweeping along both radii:

Which gives a good approximation of the mating surface. For example, with no taper you get a typical involute pattern on the outer surface since the modules along the center/outside match:

With an additional taper (pitch diameter outer vs inner illustrated here) the meshing curve is no longer involute:

I can kind of get this to work by doing successive opBoolean calls to create an approximation of the total curve, but the aliasing can get pretty bad without a very small step size:

The whole goal is to create a body that will act as the gear cutter for a ring gear, ensuring that there's no interference. Beyond the fact that opBoolean times out if you try to union more than a few surfaces, the whole recalculation is quite compute intensive and takes quite a long time to recompute (O(minutes)). Is there a way to fit a surface to this kind of approximation to avoid both the boolean ops and the aliasing? Or, alternatively, is there another approach that I'm missing that would simplify this iterative approach? I'll readily admit I'm quite new at FeatureSript; I only started messing with it for the first time this morning, so it's entirely possible there's an easier way to accomplish what I'm trying to do.
Side note: Might want to update the documentation on opLoft to include the fact that you can add a spine, but only if you also enable addSections... took me a while to figure that out
🫠
1
Comments
So the initial tooth loft itself works fine. What I'm trying to do is sweep the _resulting_ tooth loft body through a parameter sweep of two chained rotations. I can't think of an operation that would allow you to sweep a body instead of a face, so I'm approximating that sweep by iteratively generating Transforms, then copying the original body with processNewBody. That's why you're seeing a jagged aliasing in that last pic: these are independent bodies.
Ideally from these bodies I'd love to get a smooth surface that follows the outer edges of that staircase patter-... you know what? As I typed this, I think I might have solved my own question. I've previously shied away from Surface modeling, but I wonder if I can programmatically fit a surface to the edges of these bodies and use _that_ as the resulting tool...
Interesting, that might just work. Let me toy with that for a bit...