Moment of Inertia Calculations

abinand_palanisamy

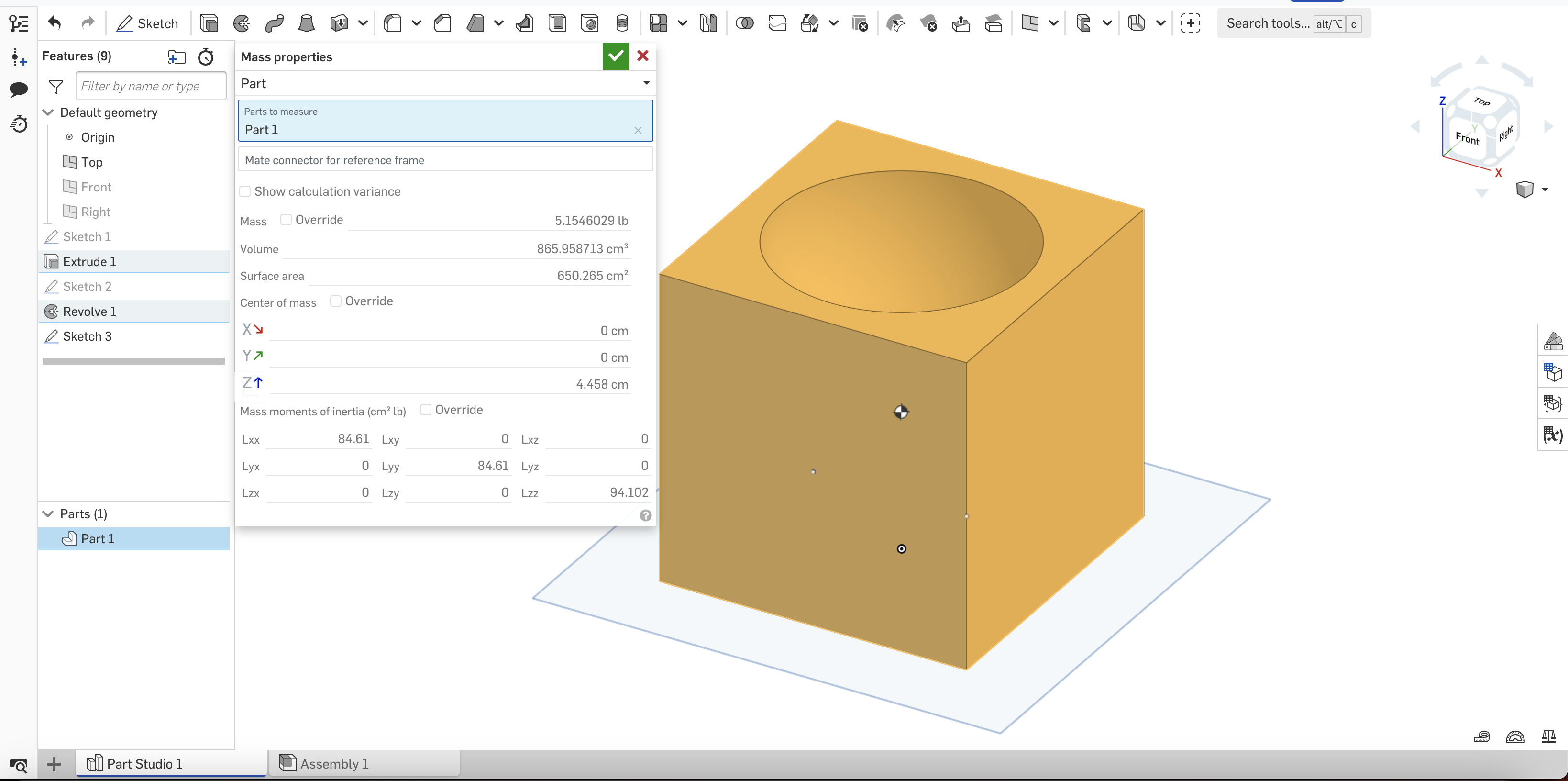
Hi everyone, I'm new to OnShape, and I have some questions on how the moment of inertia is calculated. My dimensions for this cube is 10 cm for each side length, with a diameter of 8 cm semi-sphere cut out of the top face of the cube. For example, as seen in the image, the moment of inertia along the X-axis is 84.61. Im extremely confused on how this calculation was made, as I thought the formula for moment of inertia was [(Distance from center of mass)^2] * Mass. Wouldn't this give (5^2) * 5.1546029? Is the error within my formula for the moment of inertia?

matthew_stacy

Hello @abinand_palanisamy,

Your calculation (5^2 * 5.15) describes an object with 100% of the mass (5.15 lb) located 5cm from the axis.  In actuality this mass is distributed throughout the solid, with a good portion of it located closer to the axis, reducing the mass moment of inertia.  The hole in the center affects the result as well.

Start with much simpler geometry like a cylinder to correlate your hand calculations with the Onshape result.  Note that even for a simple cylinder, spinning about the axial centerline, the value of "R" is not the full radius of the cylinder.   Sketch a circle of radius "R".  Then sketch a smaller concentric circle of radius "r_0".  Set the area of the inner circle equal to the radius of the outer circle and solve for "r_0".  This is the value that you want to use to calculate the mass-moment-of-inertia:

• π*r_0^2       = (πR^2) - (π*r_0^2)
• r_0^2           = R^2 - r_0^2
• 2 * r_0^2      = R^2
• r_0^2           = R^2 / 2
• r_0              = (R^2 / 2)^(1/2)     {or just plug the previous line for r_0^2 into your mass-moment-of-inertia formula}

If I made any errors there, I'm certain that someone will edit this for me.  Good luck @a@abinand_palanisamy

Matt_Shields

As said above, the moment of inertia for a point mass is mr^2.  Any shape where the mass is not all a constant distance, r, from the axis of rotation will involve more math.  A lot of shapes are easy to look up in a table.  Like for a rectangular cube about its center, its 1/6 ML^2.  And for a sphere (and a hemisphere) it's 2/5 Mr^2.

Onshape takes the moment of inertia about the center of mass.  So, also as said above, it's easy to verifiy this using simple shapes like cubes, spheres, and cylinders.  The center of mass of those is easy.  For your shape, it will take a few steps.

• I'd start with a cube solid and a hemispherical solid. 
• Onshape can tell you the center of mass of each.  And it will tell you the new center of mass when you subtract the hemisphere from the cube.
• Use the parallel axis theorem to find the moment of inertia of the cube and the hemisphere, each about the center of mass.
• Subtract the hemisphere MOI from the cube MOI.  You'll have to do that for each axis.  X and Y will be the same.  Z will still be in the center.

_anton

tl;dr: moment of inertia is a nontrivial integral in the general case, and computing it manually is too hard for anything but simple shapes.

abinand_palanisamy

Thanks a lot for your responses! This will for sure help me in my work so far. You guys respond so fast