Welcome to the Onshape forum! Ask questions and join in the discussions about everything Onshape.
First time visiting? Here are some places to start:- Looking for a certain topic? Check out the categories filter or use Search (upper right).
- Need support? Ask a question to our Community Support category.
- Please submit support tickets for bugs but you can request improvements in the Product Feedback category.
- Be respectful, on topic and if you see a problem, Flag it.
If you would like to contact our Community Manager personally, feel free to send a private message or an email.
New Featurescript Bezier curve. But with a twist. It has Degree control.
 Jacob_Corder
Member Posts: 141 PRO
Jacob_Corder
Member Posts: 141 PRO
I found that in the new bridging curve feature that they use a function called elevateBezier
Here is the feature to create a Bezier curve of up to degree 15 with no change in the shape. I believe @S1mon was asking for this
https://cad.onshape.com/documents/31bc937206006a84d394b252/w/64931344e2a04480f7d0eebc/e/84dff331bec6ad9f5d5e39ae
I cannot take the credit for it as the code just calls onshapes function but was not exposed in this way.
What is this features purpose? I have no idea
It also allows you to select an edge as the source the same as fit spline but only one edge

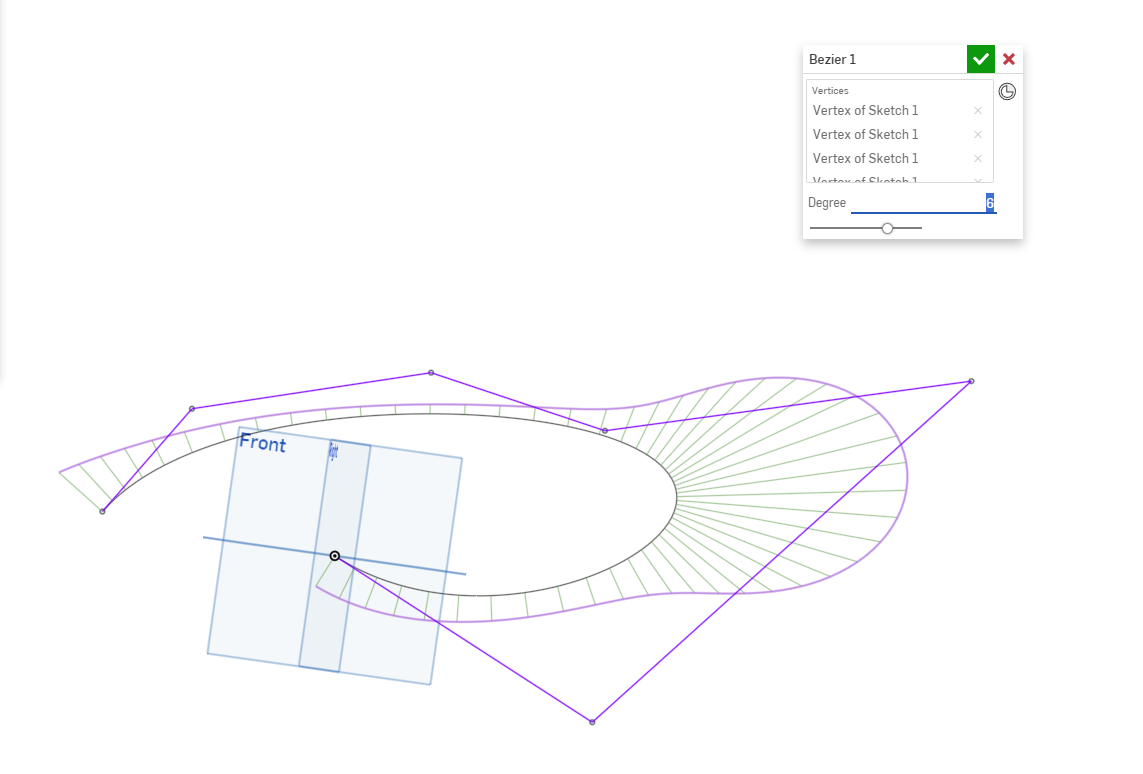
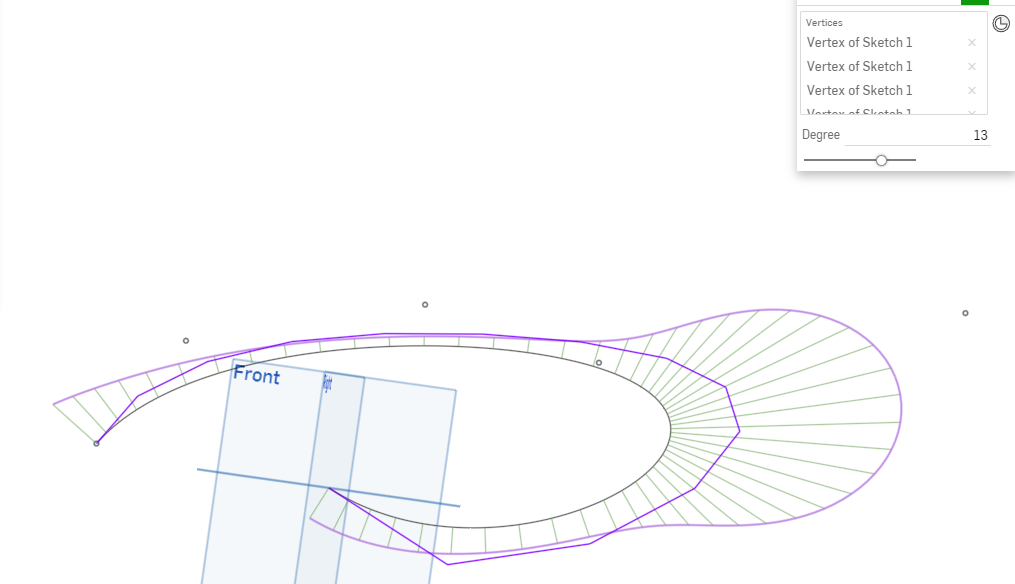
Here is the feature to create a Bezier curve of up to degree 15 with no change in the shape. I believe @S1mon was asking for this
https://cad.onshape.com/documents/31bc937206006a84d394b252/w/64931344e2a04480f7d0eebc/e/84dff331bec6ad9f5d5e39ae
I cannot take the credit for it as the code just calls onshapes function but was not exposed in this way.
What is this features purpose? I have no idea
It also allows you to select an edge as the source the same as fit spline but only one edge



3
Comments
@GregBrown and the team have clearly been working on curve tools.
Simon Gatrall | Product Development, Engineering, Design, Onshape | Ex- IDEO, PCH, Unagi, Carbon | LinkedIn
Yeah. Elevating it direct would be cool, but onshape does not allow the curves data to be modified(direct editing operations)
Regarding the youtube videos.
They are likely calling approximateSpline function in those videos for reducing the point count on those curves. That function takes the points and minimizes curvature (basically number of control points) and also allows for creating higher degree curves.
I use approximateSpline in almost all of my spline creation functions that I create for my clients. It is the fastest and only feasible way to do a degree 5 fit spline or up to degree 15 fit spline. It really is a powerful function and it is fast. Its true purpose is to generate loft profiles as it takes in points in groups to generate loft profiles of equal control point count to allow the loft feature to execute with higher quality surfaces.
Fun fact. If you pass in a degree 5 spline to boundarySurface, It will generate a degree 5 surface in that splines direction. Try it with the new bridging curve and the new g3 options and create a boundary surface. The result will be degree 7 b spline surface in one of the directions. if you create the same curves in the other direction you will get a degree 7 x degree 7 b spline surface.
My features perform the elevation or reduction using standard Bezier math, indeed I implemented my own elevateBezier initially, but just replaced it with the std library one that was recently added. The reduction uses a least squares method to try and maintain shape. In the video there are some other features (the Approximate projected curve) the do indeed use approximateSpline. BTW I agree this is a hugely useful function that more people should use as opposed to opFitSpline. There are some custom features that would really benefit from a refactoring!
I haven't shared mine publicly yet, as I'm continuing to iterate for a bit....
@GregBrown - I'm very much looking forward to seeing your code once you're ready to release. My code appears to be working, but its very slow (~10seconds runtime) - I'll be curious if/where your approach differs and captures efficiencies. I have zero experience with Bezier math (though I suspect that's about to change....), so I went about it with the tools I have on hand.
The first piece of information you need is 'how are you going to measure tolerance'? I'm not sure how approximateSpline calculates tolerance, so I created an enum in my feature that lets me specify if the user-defined tolerance refers to: 1: Maximum deviation from the curve, as measured from the .csv's input points and 2: RMS of the distances between the approximate spline and the .csv's input points. I wrote a quick and dirty function to calculate those values taking a curve body query and an array of points as input.
Create an array that will contain sub-arrays. Each row of the array corresponds to one 'guess' for the minimum value allowable in "maxControlPoints" while still staying in the tolerance window. Initialize this array with [0] -> the original number of points in the spline (same as the number of points in the input .csv file) and [1] -> the integer closest to 2/3 of this original value (I'd originally set this as half the number, but given the extreme non-linearity of the 'Tolerance to number of control point' curve, I've found better results with 2/3.
Now iterate, saving the number of control points, curve query and calculated delta in a sub-array in each iteration.
The value that we are trying to get to approach zero is the DIFFERENCE between the specified tolerance and the evaluated tolerance: (e.g) var diff = (UIspecifiedTolerance - evaluatedErrorForThisIteration'sCurve). When this value is negative, the evaluated error is LARGER than the user specified tolerance. If this value is exactly equal to 0, than the error of the approximated spline exactly matches the user specified tolerance. I found newton-rhapson iteration to be a bit brittle. I'm updating guesses by evaluating the following variables and making the following comparisons in each iteration:
var numControlPoints = number of control points for the approximated spline in each iteration; <br>var evaluatedCurveError = error between the input points from the csv file and the approximated spline; <br>var highMax = number of control points closest to zero with an evaluated error (UIDefinedTolerance - evaluatedCurveError) greater than 0;<br>var lowMax = number of control points closest to zero with an evaluated error (UIDefinedTolerance - evaluatedCurveError) less than 0;<br><br>if (evaluatedCurveError < 0 * millimeter)<br>{<br> nextGuess = ceil((highMax + numControlPoints)/2, 1);<br>}<br>else<br>{<br> nextGuess = ceil((lowMax + numControlPoints)/2, 1)<br>}This will converge on one integer value for the 'correct' number of control points. I break out of the loop for each curve when the array containing the number of control points for each guess has a duplicate value (which it ends up landing on because of the ceil function).
The results have been astonishing. As you'd expect, the wider the tolerance is set, the higher the reduction in control points. I've attached a very quick and dirty summary below - please note that the X axis is a logarithmic scale. With a 10mm tolerance, I can reduce 94% of the control points. with a .01mm tolerance, I can reduce 21% of the control points.
I hope this helps!
Simon Gatrall | Product Development, Engineering, Design, Onshape | Ex- IDEO, PCH, Unagi, Carbon | LinkedIn
if you specify interpolateIndices as every index range(0,size(points)-1) then the spline will interpolate through those points and compute the b spline curve for this Fit spline up to degree 15
Thanks!
-j