Assembly mates Revolute not solvable

gauthier_östervall

I  am trying to create a 12 sided die. The purpose is mostly to learn.

I'm trying to let Onshape calculate the angles, it's something I suppose it's good at. I created a pentagon surface in a part studio, inserted it 12 times in an assembly, and now I'm trying to give the faces some Revolute constraints in the assembly.

It's going well for a while, until I come to closing a half of the dodecahedron. Somehow the constraints are not solvable. I'm not even trying to completely close the last edge, it shouldn't be needed.



Unsuppressing Revolute 9 looks like this:


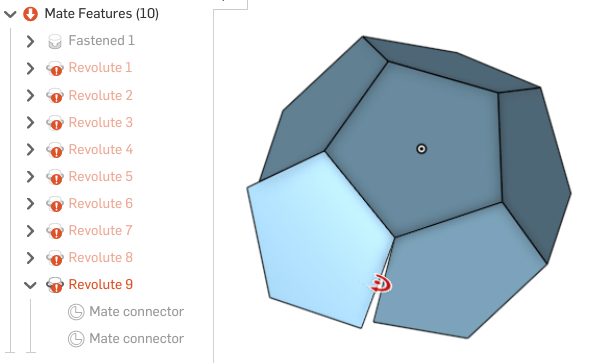
I think I'm misunderstanding something, but cannot see what.

Here is the project.

gauthier_östervall

Some clue: after fastening the "bottom" face, and suppressing the last unsolvable revolute, the last face is not rotable. Somehow, the Revolute 8 seems to fix the angle of the revolute, and I don't know why.

NeilCooke

There’s a whole dodecahedron challenge in the forums somewhere if you use the search. 

gauthier_östervall

NeilCooke said:

There’s a whole dodecahedron challenge in the forums somewhere if you use the search. 

I'm more interested in understanding Assembly and Revolute, than having an actual dodecahedron.

gauthier_östervall

I found this is trying to do nearly the same thing. It seems this isn't solved either
But trying to tie the last panel with ball mates instead of revolute still confuses the solver. Or me.

gauthier_östervall

Even with ball connectors only, this seems impossible to solve.

matthew_stacy

@gauthier_östervall, one practice that may help is to constrain, but don't OVER-constrain parts in the assembly.

Redundant constraints (attempting to control a single degree of freedom with two or more mates) will eventually result in conflicts and red ink in your assembly tree.  A rigid body has 6 degrees of freedom: x, y, z position plus rotation about each of those axes.  Once you eliminate a particular degree of freedom, do not apply additional constraints to that DoF.  The math gets a lot more complicated once you start over-constraining a structure ... that's why engineers love 'simply supported beams' but generally can't solve over-constrained beams without resorting to brute-force methods like finite-element-analysis.

For the geometry that you are attempting to create the first step is to FIX the floor, thus removing all six of its DoF.  Then place two more pentagons for the first two sides.  Mate each of these sides to the floor with a REVOLUTE mate (easier if you make the pentagon part thicker so that you can consistently select the correct inside/outside edge).  Then mate those two sides together with a BALL mate.  Onshape might let you use a REVOLUTE but eventually roundoff error in the geometry is going to result in a conflict.  Use the BALL mate!

Add the third side.  REVOLUTE mate it to the floor and BALL mate it to the adjacent side.  Continue this pattern all the way around.  Each side gets a REVOLUTE mate to the floor and a ball mate to an adjacent side.  When all is said and done DoF = 0.  The assembly is fully constrained, not over-constrained.  That's my $0.02

https://cad.onshape.com/documents/641371daf50558491bb6e53f/w/d0cfd87d405cc4d56415ecd8/e/c97338ac46e332d15ce2bb05

 

gauthier_östervall

@matthew_stacy Thanks for taking the time!! I made an attempt with only Ball mates, I had the impression that this would be the "least" strong joint, when it comes to degrees of freedom? But if failed as well.

I also tried playing with Parallel mates, I had the feeling they'd be even weaker than Ball mates.

Is there an advantage going for parts and not surfaces, like you did?

matthew_stacy

@gauthier_östervall, this assembly will work fine with surfaces or parts. 

Try dragging the pentagons closer to their final orientation and position prior to mating.  That may resolve the problem that you are having.  Imagine all 6 pentagons arranged coplanar (i.e. on the ground) with all of the sides revolute mated to the floor.  There are two possible solutions.  The sides can be hinged up or down.  Dragging the sides into rough alignment prior to mating removes possible ambiguity.

Don't mess with parallel mates.  For this model you want 5 revolutes (sides to bottom) and 4 ball mates (side to side).

Good luck!

gauthier_östervall

Thanks for the hints, it's helpful.

You're right that parallel mates couldn't work it out. I don't get why though, they should be less restrictive than ball mates?

I could do to halves of the dodecahedron, but not put them together. I did move the surfaces in a position that was close to the desired result. Strangely, when I add a mate (ball mates to as few corners as possible) and the solver fails, removing the new mate leaves the Assembly inconsistent on the first steps...

matthew_stacy

@gauthier_östervall, if you want to share document edit privileges with me (matthew.g.stacy@outlook.com) we can arrange a time to get in the document simultaneously and use tools like "follow mode" to figure this thing out.  Onshape has unrivaled collaboration tools for exactly this sort of thing.