G³ Constraint for Bézier?

S1mon

Given a Bézier which is degree n (and in this case n≥3), if I want to make the P₀ end point G² to another curve, I know that there's a simple equation. Let c= distance from P₀ to P₁, d= normal distance of P₂ from the P₀-P₁ vector, and 𝜅 is the curvature of the adjoining curve at the common endpoint. Then d=(n/(n-1))𝜅c². Is there a similar simple equation for a G³ constraint for the P₃ point?

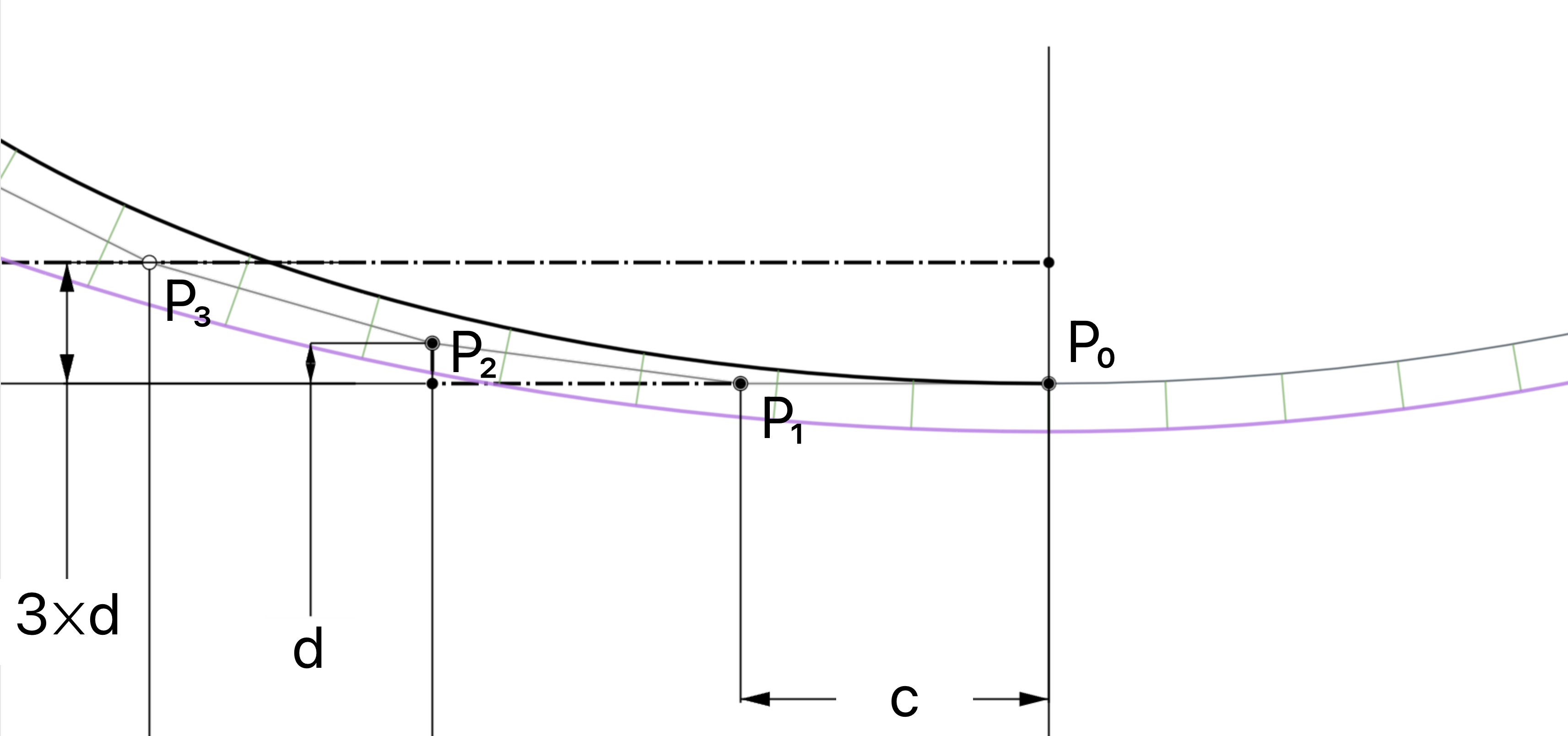
From what I've seen so far, if the adjoining curve has constant curvature (i.e. jolt is 0), then P₃ lies on a line 3d from the P₀-P₁ vector.

S1mon

On further experimentation, it seems P₃ works like this iff P₂ is 2⨉c from P₀. Otherwise the 3⨉d dimension must also change. I don't yet have that relationship worked out.

Jacob_Corder

Watch this video. the answer is probably in it somewhere at the end. She explains up to G3 and C3 and how to achieve it
https://youtu.be/jvPPXbo87ds

You can also look how the bridging curve code extracts G2 continuity. 

what possible reason do you have to need G3 control?  That is going to create one complex curve. 

S1mon

I'm pretty familiar with Freya's work - I was one of a very large group of Patreons that supported this work. I posted this video here recently. She does a good job explaining parametric vs geometric continuity and some stuff about what it takes to achieve each. However, if I'm trying to make a new curve G³ to two existing curves/edges, those driving curves may not also be Béziers. I can extract the curvature at the end point using evEdgeCurvatures(), but there's no built in tool to extract the jolt. Extracting the control points, knots, and weights of an arbitrary NURBS curve is not really helpful given the mathematical complexity of anything other than a Bézier.

G³ (and sometimes higher) are necessary to do class-A surfacing for industrial design. Rhino, Creo, Alias, Icem, Solidworks, Nx, Catia, etc all have G³ constraints. If you want the zebra stripes to be ≥G², you need the surfaces to be ≥G³.

Jacob_Corder

Freya is great. I watched that video 2x. 

I have never come across any code to even extract the G2 continuity let alone the jolt.  Hopefully someone on here has and can supply it to us. 
I think you need to establish some sort of rules for your requirement.

Another option is to import a curve from one of the other systems and import it and analyze how that cad engine decided to generate that curve.  If it does not import as a BSpline curve and needs to be analyzed using evApproximateBSplineCurve, then export it as a step file(just the curve) and you can read the b spline curve data in the step file by opening it with notepad.  Then reverse engineer it somehow to determine how they determine where the control points are placed.

If you don't have access to any of those cad systems, which i dont either, then hopefully someone can give you a step file with the curves you need to reverse engineer it.

S1mon

G2 is in Bridging curve. 

    // using k = ((degree - 1) / degree) * h / |t| ^ 2, where k is curvature, t is tangent vector, h is the minimum distance
    // from the next control point to the extension of tangent direction
    var distance = (degree / (degree - 1)) * curvatureFrame.curvature * speed * speed;

Below is from Thomas W Sederberg's Computer Aided Geometric Design (a free-to-download 273 page book which is a great reference on Béziers, B-Splines, etc). Assuming that we're using non-rational Béziers, you can ignore the first term in the 2.13 equation, and that's the same as what's in the Bridging curve code. "speed" is a in the diagram below, "distance" is h. The Bridging curve equation has just solved 2.13 for h instead of k.

Nick_Holzem

@S1mon, I have been looking for a way to artificially match curve acceleration between arcs using a bezier curve. Have you found any easy button for this? Here's a look at my sketch. I'd like the acceleration to match at these points. I've been experimenting with number control points and different patterns and constraints to achieve this but can't seem to get it right. Is this even possible? 

S1mon

@Nick_Holzem

You need a minimum of 3 control points beyond where the Bézier joins the arc in order to match g3. When matching the acceleration of an arc or line, that derivative is zero. ie the change in curvature is zero at the point where the spline joins an arc or line.

At bare minimum, you need a degree 5 Bézier to make a g3 transition between an arc and a line. The arc and the line need to be in a good arrangement to do this with only a degree 5. For arbitrary pairs of arcs and lines you'll need a degree 7 curve.

Look very carefully at the parallel/equal/perpendicular constraints on the helper lines attached to the spline going into the arc (zoomed in below). This technique is useful when connecting to an arc or if a spline ends at a mirror plane. The spline is also constrained to be curvature to the arc. The curvature constraints in Onshape are very twitchy. Sometimes you will need to delete and re-apply them or move the spline around until it's close to being g2 before adding the constraint. Other times you'll make a very minor adjustment to one of the dimensions and the whole sketch will go red. You can undo the change or delete the curvature constraint and move things around and try again. In general, I try to dimension as few control points as I can get away with, and use constraints and the solver to fill in the unknowns.

Here's a pass at something similar to your example:

There is an arc at the left/right and then the top and bottom are composed of degree 6 curves which are mirrored. I used the technique from above going into the arc and to the mirror plane.

Here's a link to the document with these examples: https://cad.onshape.com/documents/dd14aa1da5699201425d5ef9/w/c78da12d1b52c9a35611d128/e/b937fac6e30a58034b3b62b9

Also, I highly recommend some of the essentials training for Alias. 

https://help.autodesk.com/view/ALIAS/2024/ENU/?guid=cvs-hulls-and-degree (Look at the section called "Deep Dive: Flow of CVs and Hulls" in particular)
https://help.autodesk.com/view/ALIAS/2024/ENU/?guid=continuity-g0-g1-g2-g3 (Look at the section "Deep dive: G3 and G4 continuity")

S1mon

I just added another sketch which perhaps solves your problem, but ignores the solution you were going after. 

You can add internal constrains like coincident or normal to a spline and control where and how the curve flows in the middle. Here I've constrained the left extreme with a coincident and normal to control where the tightest part of the curve is. The 150 and 75 control where the curve flows through. I don't have direct control over that radius, but by tweaking the control point dimensioned by the 41 and 19, I can exert some control over the minimum radius, as shown by the curvature evaluation tools. Meanwhile the whole 1/2 of the shape is one degree 6 Bézier, which is by definition, g-infinity within itself. 

Nick_Holzem

@S1mon Wow! this is great stuff. Exactly what I was looking, I owe you beer or two for sure! Next time you're in Wisconsin reach out. I'll be applying these schemes to my model today, and sharing your approaches with my team. The more I work with surfacing in Onshape the more I see the importance of higher continuity in sketches and curves. Thank you!